Il problema delle donazioni di reni
Nella lezione inaugurale del corso di algoritmi presso il Collège de France, Claire Mathieu, nota ricercatrice francese nell’ambito degli algoritmi di approssimazione e degli algoritmi on-line (e non solo), descrive un esempio molto bello di come il metodo informatico opera di fronte a problemi reali. In particolare, Claire fa riferimento al problema della donazione di organi e, più specificamente, alla donazione di reni. Cercheremo ora di spiegare nel modo più semplice possibile la modellazione del problema, la progettazione di un algoritmo che lo risolva e la sua implementazione. Per chi voglia, invece, vedere subito tali aspetti e per chi non ha difficoltà a capire il francese, consigliamo di “gustarsi” la bellissima lezione di Claire.

Ciascun essere umano ha, normalmente, due reni a disposizione e può, se lo desidera, donarne uno a un altro essere umano che si trovi nella necessità di averne bisogno. La lista di persone in attesa di un donatore aumenta nel corso degli anni e il problema che dobbiamo risolvere è quello di organizzare la lista dei donatori e quella delle persone in attesa in modo da sfruttare al meglio le opportunità di donazione. Infatti, il trapianto può avvenire solo in determinate condizioni di compatibilità tra il donatore e il ricevente (oltre, ovviamente, alla disponibilità da parte del donatore di trapiantare un suo rene in una specifica persona).
Supponiamo, come mostrato nella figura seguente, che Alice voglia donare un rene al suo amico Bruno e che Carlo voglia donare un rene al suo amico Davide. Tuttavia, per problemi di compatibilità, queste due donazioni non posso avere luogo. Se, però, il rene di Alice è compatibile con Davide e quello di Carlo è compatibile con Bruno, allora è possibile effettuare allo stesso tempo i due trapianti “incrociati”, come mostrato nella figura. Il problema diventa, pertanto, quello di trovare il maggior numero di incroci di questo tipo che esistono nella lista delle coppie dei potenziali donatori e dei corrispondenti potenziali riceventi.
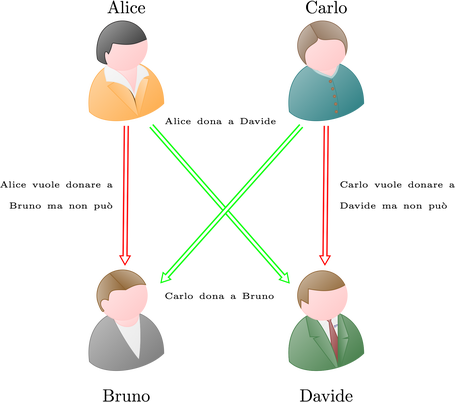
Tale problema può essere formulato facendo, ancora una volta, uso di uno degli ingredienti di base introdotti nel primo capitolo del libro: i grafi. Infatti, ciascuna coppia formata da un donatore D e dal ricevente R a cui D è disponibile a donare un proprio rene (ma non può farlo per motivi di compatibilità) diviene un nodo di un grafo. Esiste poi un arco tra il nodo corrispondente alla coppia (D1, R1) e quello corrispondente alla coppia (D2, R2) se il rene di D1 è compatibile con R2 e se il rene di D2 è compatibile con R1. Nell’esempio precedente, il grafo contiene i due nodi (Alice, Bruno) e (Carlo, Davide) ed esiste un arco che connette questi due nodi. Il problema dell’organizzazione delle donazioni di reni diventa, allora, quello di trovare un cosiddetto accoppiamento massimo, ovvero un insieme di archi che non si “toccano”, che sia il più grande possibile. Ognuno di questi archi inclusi nell’accoppiamento corrispondono a un trapianto incrociato di reni, come quello tra Alice e Davide e tra Carlo e Bruno che abbiamo visto nell’esempio precedente.
Per esempio, se consideriamo il grafo mostrato nella parte sinistra della figura seguente, l’insieme formato dagli archi in rosso nella parte centrale della figura è un accoppiamento, ma non è massimo. Infatti, l’insieme degli archi in rosso mostrati nella parte destra della figura è anch’esso un accoppiamento ma più grande (vi invitiamo a verificare che questo secondo accoppiamento è anche quello più grande possibile).

Abbiamo dunque visto che il problema di organizzare in modo efficace le donazioni di reni si riduce al problema di calcolare in un grafo un accoppiamento massimo. Descriviamo ora un algoritmo per eseguire tale calcolo.
Per spiegare tale algoritmo, facciamo però riferimento al caso particolare in cui il grafo sia bipartito, ovvero in cui i nodi del grafo siano suddivisi in due insiemi C e S e gli archi possano connettere solo nodi in C con vertici in S. Per esempio, il grafo mostrato nella figura seguente è un grafo bipartito in cui l’insieme C contiene 7 nodi, l’insieme S contiene 5 nodi e vi sono 11 archi.
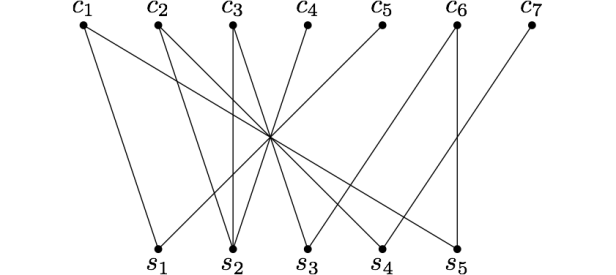
L’algoritmo per il calcolo dell’accoppiamento massimo procede per miglioramenti successivi: in particolare, dato un accoppiamento M che non sia massimo, ci domandiamo come sia possibile migliorarlo. Facendo riferimento al grafo della figura precedente, consideriamo, per esempio, l’accoppiamento M mostrato nella figura seguente: a prima vista, potrebbe sembrare che non ci sia nulla da fare per migliorare quest’accoppiamento, in quanto il nodo s5 può solo accoppiarsi con i nodi c1 e c6, i quali tuttavia sono già accoppiati con i nodi s1 e s3, rispettivamente. Pertanto, se vogliamo migliorare tale accoppiamento dobbiamo in qualche modo modificare gli accoppiamenti già esistenti, in modo da aumentare il numero degli accoppiamenti totali.
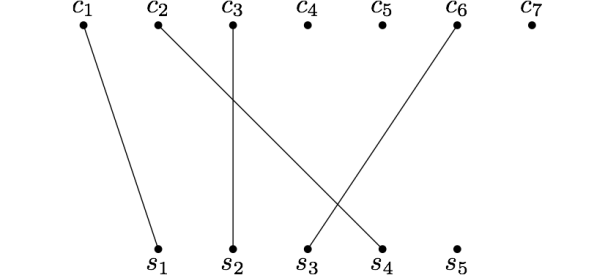
A tale scopo, consideriamo un nodo dell’insieme C non ancora accoppiato, come, per esempio, il nodo c4: per poter accoppiare tale nodo, dobbiamo farlo necessariamente con il nodo s2, il quale però è già accoppiato con il nodo c3. Proviamo allora a separare s2 da c3 e ad accoppiare c3 con qualche altro nodo, che necessariamente deve essere s3. Anche in questo caso, s3 è già accoppiato con c6: per accoppiare c3 e s3, separiamo s3 da c6 e proviamo ad accoppiare c6 a qualche altro nodo. Finalmente, c6 può accoppiarsi con s5 che è al momento libero. Abbiamo così trovato un accoppiamento migliore (si veda la figura seguente), in cui tutti i nodi di S sono accoppiati: per questo motivo, tale accoppiamento è anche quello massimo.
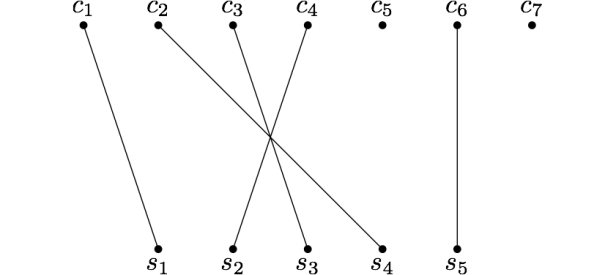
Il nuovo accoppiamento è stato trovato seguendo un cammino che partiva da un nodo dell’insieme C non ancora accoppiato, che terminava in un nodo dell’insieme S non ancora accoppiato e che alternava il percorrere un arco non incluso nell’accoppiamento con il percorrere uno incluso nell’accoppiamento: tale cammino è mostrato nella figura seguente, in cui gli archi percorsi dal cammino non inclusi nell’accoppiamento sono disegnati tratteggiati.
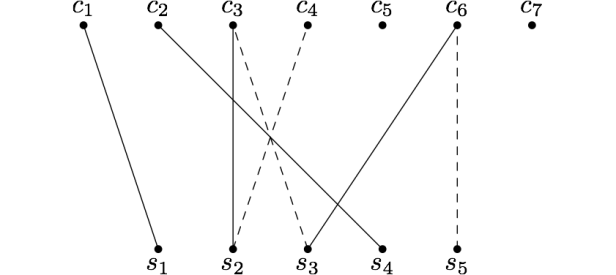
Un cammino che alterna archi non nell’accoppiamento con archi nell’accoppiamento è chiamato cammino alternante rispetto all’accoppiamento. Un cammino alternante in cui il primo e l’ultimo nodo non sono accoppiati è chiamato cammino aumentante, in quanto un tale cammino implica sempre che l’accoppiamento può essere migliorato togliendo da esso tutti gli archi del cammino che ne facevano parte e aggiungendo a esso tutti gli archi del cammino che non ne facevano parte: poiché il cammino inizia da un nodo dell’insieme C e termina in un nodo dell’insieme S, il numero di archi che vengono aggiunti è sempre maggiore di quello degli archi che vengono tolti, per cui il nuovo accoppiamento ha un arco in più.
Quest’osservazione suggerisce un algoritmo per cercare un accoppiamento di cardinalità massima: tale algoritmo, anche noto come algoritmo di Ford-Fulkerson, procede nel modo seguente.
- Inizializza M ponendolo uguale all’insieme vuoto.
- Cerca un cammino p aumentante rispetto a M: se tale cammino non esiste, allora restituisce M come accoppiamento finale e termina.
- Altrimenti, toglie da M tutti gli archi di p che appartenevano a M, aggiunge a M tutti gli archi di p che non appartenevano a M e ritorna al passo precedente.
È possibile dimostrare che l’accoppiamento restituito da tale algoritmo è il massimo possibile: in particolare, si può dimostrare che se non esiste un cammino aumentante rispetto a M, allora M è massimo. Osserviamo che tale algoritmo si estende a grafi generali e non solo bipartiti: tale estensione è nota come algoritmo dei cammini, alberi e fiori, è stato ideato da Jack Edmonds negli anni sessanta e può essere usato per risolvere il problema della donazione di reni, il cui corrispondente grafo non è detto che sia bipartito.

Il programma che realizza l ‘algoritmo di Ford-Fulkerson fa uso di due funzioni. La prima funzione, che si chiama massimoaccoppiamento, parte dall’accoppiamento vuoto, verifica se esiste un nodo c non accoppiato a partire dal quale esista un cammino aumentante. Se così è l’accoppiamento viene aggiornato e questo passo viene ripetuto fino a quando non esiste alcun nodo c non accoppiato dal quale sia possibile far partire un cammino aumentante. La seconda funzione, che si chiama camminoaumentante, calcola, se esiste, un cammino aumentante rispetto all’accoppiamento attuale che parta dal nodo c. A tale scopo, per ogni vicino s di c, verifica se tale vicino non sia accoppiato: in tal caso, c viene accoppiato a s (e viceversa) e la funzione restituisce il valore true. Altrimenti, se s è accoppiato con un nodo diverso da c, la funzione verifica ricorsivamente se esiste un cammino aumentante a partire da tale nodo: in tal caso, c viene accoppiato a s (e viceversa) e la funzione restituisce il valore true. Se non si riesce a trovare alcun vicino di c da accoppiare a c stesso, allora vuol dire che non esiste un cammino aumentante a partire da c e la funzione restituisce il valore false. Per evitare di “ripassare” per gli stessi nodi, il nodo c e il nodo s vengono marcati come visitati.
Per esempio, consideriamo il grafo mostrato nella parte sinistra della figura seguente. La funzione massimoaccoppiamento inizializza l’accoppiamento ponendolo uguale a quello vuoto, come mostrata nella parte destra della figura.
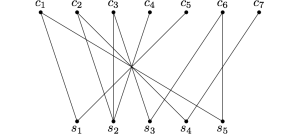

Successivamente, viene invocata la funzione camminoaumentante con input il nodo c1 che trova un cammino aumentante formato dal solo arco che congiunge c1 a s1 e aggiorna quindi l’accoppiamento che diventa quello mostrato nella parte sinistra della figura seguente.


Poiché l’accoppiamento è stato migliorato, la funzione massimoaccoppiamento continua a cercare un nodo non accoppiato da cui far partire un nuovo cammino aumentante. Viene quindi invocata nuovamente la funzione camminoaumentante con input il nodo c2 che trova un cammino aumentante formato dal solo arco che congiunge c2 a s2 e aggiorna quindi l’accoppiamento che diventa quello mostrato nella parte destra della figura precedente.
Alla successiva invocazione della funzione camminoaumentante, con input il nodo c3, viene trovato un cammino aumentante che passa per i nodi c3, s2, c2 e s4, come mostrato nella parte sinistra della figura seguente. Tale cammino aumentante modifica l’accoppiamento nel modo mostrato nella parte destra della figura.

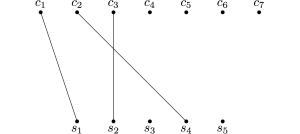
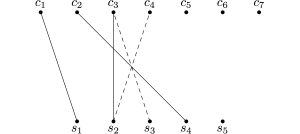
Alla successiva invocazione della funzione camminoaumentante, con input il nodo c4, viene trovato un cammino aumentante che passa per i nodi c4, s2, c3 e s3, come mostrato nella parte sinistra della figura seguente. Tale cammino aumentante modifica l’accoppiamento nel modo mostrato nella parte destra della figura.
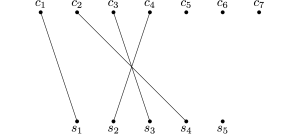
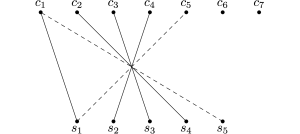
Infine, alla successiva invocazione della funzione camminoaumentante, con input il nodo c5, viene trovato un cammino aumentante che passa per i nodi c5, s1, c1 e s5, come mostrato nella parte sinistra della figura seguente. Tale cammino aumentante modifica l’accoppiamento nel modo mostrato nella parte destra della figura: tale accoppiamento è chiaramente massimo in quanto tutti i nodi della parte bassa del grafo sono accoppiati.
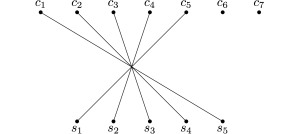
Cosa possiamo dire riguardo al tempo di esecuzione di questo programma? Anzitutto osserviamo che la funzione massimoaccoppiamento ripete la ricerca di un miglioramento dell’accoppiamento attuale al più tante volte quanti sono i nodi della parte più piccola del grafo (nel nostro esempio S), in quanto a ogni miglioramento un nuovo nodo di questa parte viene accoppiato. Ogni ricerca di un miglioramento può richiedere un numero di invocazioni della funzione camminoaumentante pari al più al numero di nodi nella parte più grande del grafo (nel nostro esempio C). Infine, ogni invocazione della funzione camminoaumentante richiede al più un numero di operazioni proporzionale al numero di archi del grafo, in quanto ogni nodo viene “visitato” una e una sola volta. In conclusione, possiamo concludere che il tempo di esecuzione del programma è proporzionale a n2m, dove n indica il numero di nodi del grafo e m il numero di archi. In realtà è possibile fare di meglio, ma già questo programma e quest’analisi ci permette di concludere che il problema del calcolo del massimo accoppiamento in grafi bipartiti è un problema “facile”. In realtà, lo stesso risultato vale anche per il problema nel caso di grafi generali e, quindi, possiamo concludere che il problema dell’organizzazione dei trapianti di reni, modellato come un problema di calcolo dell’accoppiamento massimo, rientra nella categoria dei problemi “facili”.
