La macchina di Turing
Nella nota all’inizio del quinto capitolo, diciamo che la domanda che Turing si pose era, più precisamente, «le macchine possono pensare?» Oggigiorno, quello che Turing chiama macchina non è altro che un computer, ma nel suo articolo Turing faceva riferimento a un modello di calcolo da lui stesso definito alcuni anni prima.
Una macchina di Turing è un dispositivo che può trovarsi in un certo numero di stati, ha a disposizione un foglio a quadretti grande a piacere e, in ogni istante, si trova posizionato su un quadretto specifico, in cui c’è scritto un simbolo. Sulla base dello stato in cui si trova e del simbolo letto nel quadretto al momento considerato, la macchina decide eventualmente di sostituire tale simbolo con un altro simbolo, di spostare la sua attenzione su un altro quadretto e di cambiare il proprio stato.
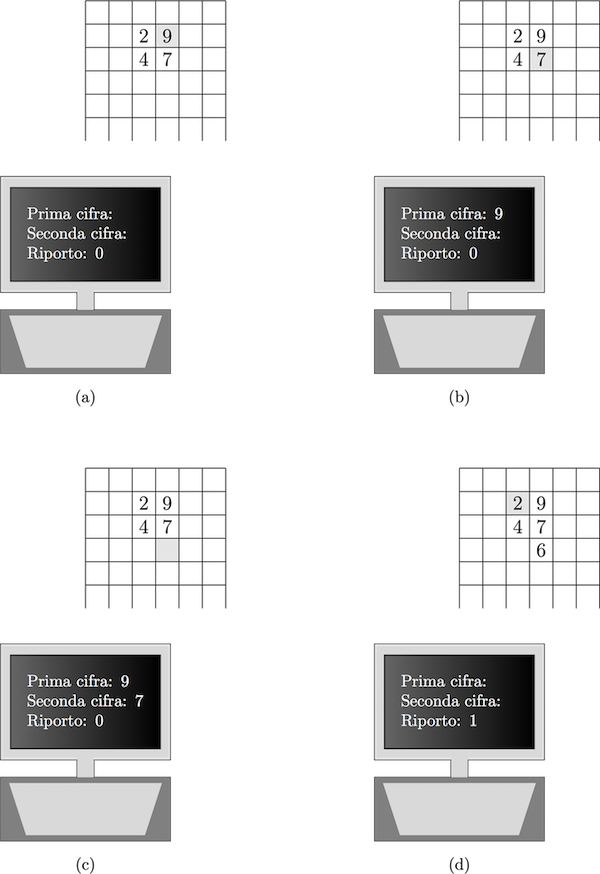
La specifica di un tale dispositivo si ispira al modo naturale degli esseri umani di eseguire dei calcoli. Si pensi, per esempio, all’operazione di somma di due numeri interi, così come ci viene normalmente insegnata alla scuola elementare. In questo caso, il nostro stato mentale memorizza le cifre da dover sommare e l’eventuale riporto. A ogni passo della somma eseguiamo il seguente algoritmo (si veda la figura che segue).
- Leggi la cifra d1 più a destra del primo numero non ancora esaminata e memorizzala.
- Leggi la cifra d2 più a destra del secondo numero non ancora esaminata e memorizzala.
- Somma d1, d2 e il riporto (che inizialmente è 0), scrivi la cifra delle unità del risultato nella posizione libera pià a destra della somma e memorizza il riporto, che può essere 0 o 1, e ricomincia.
Per capire meglio il funzionamento di una macchina di Turing, consideriamo un problema più facile della somma, ovvero il problema seguente: data una sequenza di 0 e 1, si vuole verificare se il numero di 1 è dispari.
Supponiamo che la sequenza sia scritta orizzontalmente nel foglio a quadretti, con un simbolo, per quadretto. La macchina parte dal primo simbolo della sequenza e si sposta da sinistra verso destra. Per ogni simbolo letto, controlla se è 0 o 1. Se vede un 1, la macchina si ricorda che il numero di 1 visto finora è pari se precedentemente era dispari oppure è dispari se era pari. Infine, la macchina si sposta di un quadretto a destra.
Questo comportamento può essere definito più precisamente nel modo seguente. L’alfabeto di simboli della macchina è {0,1,#}, dove il simbolo #, posto alla fine della sequenza, serve per comunicare che la verifica è conclusa. Gli stati in cui la macchina può trovarsi sono i seguenti:
- I: lo stato iniziale;
- P: questo stato indica che la macchina ha letto sinora un numero pari di 1;
- D: questo stato indica che la macchina ha letto sinora un numero dispari di 1;
- F: lo stato finale.
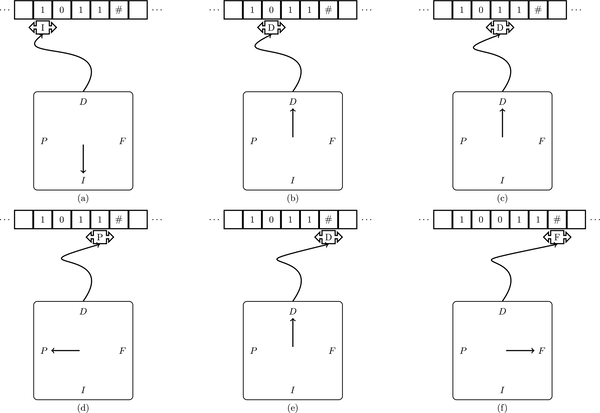
Come mostrato nella figura che segue (parte (a)), all’inizio la macchina è posizionata sul primo simbolo della sequenza e si trova nello stato I. Se la macchina legge 0 passa allo stato P e si sposta a destra di un quadretto, mentre se legge un 1 (come nel caso della parte (a) della figura) passa allo stato D e si sposta di un quadretto a destra (si veda la parte (b) della figura). La successiva lettura di uno 0 (come nel caso della parte (b) della figura) farà restare la macchina nello stato dove si trova, mentre quella di un 1 la farà passare allo stato P (se era nello stato D) o allo stato D (se era nello stato P). Adesso il meccanismo generale è chiaro: se incontra uno 0, la macchina resta nello stato dove si trova, se incontra un 1 e si trova nello stato D passa allo stato P e viceversa (si vedano le parti (c)-(e) della figura). La verifica termina con successo, quando la macchina legge #, si trova nello stato D e si porta nello stato finale (si vedano le parti (e)-(f) della figura).
Se, come abbiamo visto, una macchina di Turing è capace di fare le somme, è anche in grado di fare le moltiplicazioni, in quanto il prodotto di due numeri n e m è uguale alla somma di n con se stesso eseguita m volte. Se è capace di fare le moltiplicazioni, può fare l’elevamento a potenza, in quanto la potenza nm è uguale al prodotto di n per se stesso eseguito m volte. In altre parole, la macchina di Turing, pur nella sua semplicità, è in grado di fare della matematica ragionevolmente complicata.
Turing ne capì appieno le potenzialitè al punto da introdurre il concetto di macchina di Turing universale, che oggi chiameremmo sistema operativo (come, ad esempio, Linux e MacOS X). L’idea di base è che una macchina di Turing è una sequenza di caratteri rappresentanti le istruzioni che la macchina deve eseguire, come quelle descritte sopra per la somma o per la verifica che il numero di 1 in una sequenza di 1 e 0 sia dispari. Pertanto può essere essa stessa oggetto di elaborazione da parte di un’altra macchina di Turing, al pari delle cifre decimali su cui opera la macchina per fare la somma o dei simboli 1, 0 e # su cui opera la macchina per verificare se il numero di 1 è dispari.

La macchina di Turing universale, in particolare, è in grado di leggere una qualunque altra macchina di Turing e simularne l’esecuzione con input una qualunque sequenza finita di simboli (si veda la figura precedente). Come già detto, tale macchina è la madre del software dei nostri odierni computer, siano essi desktop, laptop, tablet o smartphone. Gli enormi sviluppi tecnologici che hanno fatto seguito, senza modificare troppo l’impianto dato da Turing, hanno principalmente consentito la progettazione e lo sviluppo di computer che entrassero nelle nostre borse e perfino nelle nostre tasche.
